Last updated on 2024-7-10…
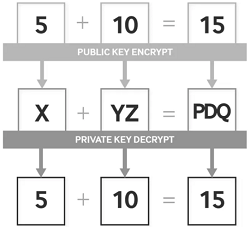
同态加密(Homomorphic encryption)是一种加密形式,它允许人们对密文进行特定形式的代数运算得到仍然是加密的结果,将其解密所得到的结果与对明文进行同样的运算结果一样。换言之,这项技术令人们可以在加密的数据中进行诸如检索、比较等操作,得出正确的结果,而在整个处理过程中无需对数据进行解密。其意义在于,真正从根本上解决将数据及其操作委托给第三方时的保密问题,例如对于各种云计算的应用。
第一代FHE
1978 年,在 RSA 方案发布后的一年内,RL Rivest、L. Adleman 和 ML Dertouzos首次提出了构建完全同态加密方案的问题。
2010 DGHV
Gentry基于理想格(Ideallattice)构造出了第一个可行的全同态加密方案,该方案中先构造了一个有限层次全同态加密方案,然后通过自举实现全同态加密,该构造全同态加密的框架成为后续大多数方案的重要思路,从而全同态加密被冠以“密码学的圣杯”。
Gentry于2010年提出基于整数的全同态加密方案DGHV,仅在整数上进行简单计算,其安全性可以归约为近似最大公约数问题,然后使用自举实现全同态加密。因此,DGHV方案被认为是第一代全同态加密方案的代表。
第二代FHE(环上整数加密)
所有的第二代密码系统仍然遵循 Gentry 原始结构的基本蓝图,即它们首先构建一个部分同态的密码系统,然后使用引导将其转换为完全同态的密码系统。第二代密码系统的一个显著特征是,它们在同态计算过程中都具有噪声增长速度慢得多的特点。
2011 BGV
2011年 Brakerski-Gentry-Vaikuntanathan 提出 Fully Homomorphic Encryption without Bootstrapping,BGV方案在IBM Research的HElib库和新泽西理工学院的PALISADE库/框架中实现
BGV基于“Learning With Errors”(LWE)问题,算法将明文信息编码在密文的最低比特位上,使用模数切换技术来控制噪声增长。BGV算法在处理大规模数据集时可能面临性能挑战,但其解密过程相对简洁高效,适用于需要确定性加密方案的场景,如有限域上的多方计算(MPC)与同态加密(HE)结合的场景。

2012 BFV
2012年 Brakerski-Fan-Vercauteren 提出 Somewhat Practical Fully Homomorphic Encryption,BFV方案在Microsoft SEAL,PALISADE和FV-NFLlib库中实现
BFV算法基于“Ring-Learning With Errors”(RLWE)问题,最初由Zvika Brakerski在2012年提出,算法将明文信息编码在密文的最高比特位上,通过缩小操作来控制噪声,密文模数Q固定,所有的密文在做乘法后都会缩小Q/p而噪声逐渐增加(p是明文模数)。 BFV适用于需要对加密数据进行复杂计算的场景,尤其是在明文空间较大时。
第三代FHE(二进制加密)
GSW加密体系
2013 年,Craig Gentry、Amit Sahai 和 Brent Waters (GSW)提出了一种构建 FHE 方案的新技术,引入了近似的特征向量方法消除了对密钥切换和模数转换技术的要求。这种技术将同态乘法引入的误差增长降低到一个小的多项式系数上。
AP/GINX加密体系
GSW方案后续进一步改进,2014年Alperin-Sheriff和Peikert 提出了一 种新的自举算法AP,将解密视为一种算术电路而不是布尔电路。基于该自举算法,2015年Ducas 等人提出方案杜卡斯-米奇安西奥同态加密档案 (Ducas-Micciancio scheme, DM/FHEW),该方案使得全同态自举能力得到了大幅度提升。之后, Chillotti等人基于另一种自举方案(Gama-Izabachène-Nguyen-Xie scheme, GINX),对FHEW方案进行优化,提出 了TFHE方案。
2014 FHEW
2014 年 FHEW: Bootstrapping Homomorphic Encryption in Less Than a Second,代码:https://github.com/lducas/FHEW
FHEW(Fast Homomorphic Encryption with Weights)是一种快速的带权全同态加密方案,特别适用于处理大量二进制数据的同态计算。
2015 TFHE
2015年 TFHE: Fast Fully Homomorphic Encryptionover the Torus,代码:https://github.com/tfhe/tfhe
NuCypher公司提供了基于TFHE的GPU实现:https://github.com/nucypher/nufhe
TwC Group东华集团提供了基于TFHE的多GPU实现:https://github.com/TrustworthyComputing/REDcuFHE
Torus FHE 方案进一步提高了FHEW的效率,该方案使用类似于FHEW中的方法实现了自举过程的环形变体。TFHE自举的基本思路是借助基于GSW的同态乘法在多项式的幂次上运行LWE解密算法。TFHE 的自举方案如图4所示,TFHE自举中最核心的部件是盲旋转,也叫同态累加。
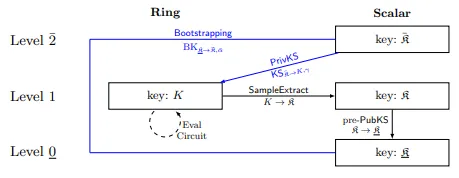


针对二进制密钥而言,TFHE比FHEW更快,且不受密钥大小的影响;而对于更高的密钥大小(三进制以上),FHEW的运行时间优于TFHE。此外,在内存方面,TFHE具有比FHEW更小的自举密钥。
第四代FHE(浮点数编码加密)
2016 CKKS
2016年 Homomorphic Encryption for Arithmetic of Approximate Numbers,CKKS在Microsoft SEAL,HEAAN和HElib中实现
微软公司提供了CKKS的具体实现:https://github.com/Microsoft/SEAL
Desilo公司提供了基于CKKS的多GPU实现:https://github.com/Desilo/liberate-fhe
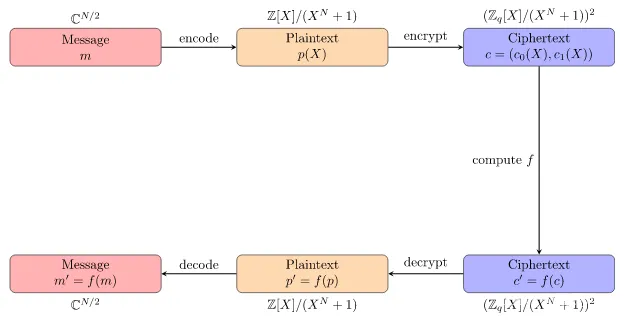
该方案支持一种特殊的定点算法,通常称为块浮点算法。CKKS 方案包括一个高效的重缩放操作,该操作在乘法后缩减加密消息。相比之下,这种重新缩放需要在 BGV 和 BFV 方案中进行引导。重缩放操作使 CKKS 方案成为评估多项式近似的最有效方法,并且是实现隐私保护机器学习应用程序的首选方法。

简要总结

- BGV和BFV方案适用于有限域上的计算,并具备高效的打包功能,但其不适用于具有大型乘法深度的电路或需要实现非线性函数的电路
- CKKS方案可以处理实数域上的计算,但是对于整数域上的精确计算存在局限性
- TFHE方案能够快速评估布尔电路,但其不支持批处理操作,无法同时处理同时大量数组
后续论文收录
基于RLWE的全同态加密方案能够支持单指令多数据技术进行并行计算。但由于在多项式环上的算术限制,基于RLWE的方案难以对逻辑函数进行计算。
基于LWE的全同态加密方案支持在布尔电路评估中快速自举。但明文空间小,难以支持密文乘法,并且无法进行批处理操作。
于是想到了多项式算子与逻辑算子转换。
2020 CHIMERA
2020年 CHIMERA: Combining Ring-LWE-based Fully Homomorphic Encryption Schemes
每种类型的方案有不同的优势:
- BGV/Helib 方案:善于使用 SIMD 在有限域上进行计算
- B/FV 方案:善于使用 SIMD 在向量模 p 上进行计算
- HEAAN(CKKS) 方案:善于使用 SIMD 进行定点数运算
- TFHE 方案:善于按位评估、计算布尔逻辑、比较、阈值计算、计算复杂电路等…
有没有什么方法能够使用这些方案的优势,同时避免它们的劣势呢?Mariya Georgieva 等人给出了一个解决方案:
- 在环面上定义明文空间
- 在密文表达之间转换
- 在 TFHE 、B/FV 、HEAAN 之间建立桥梁
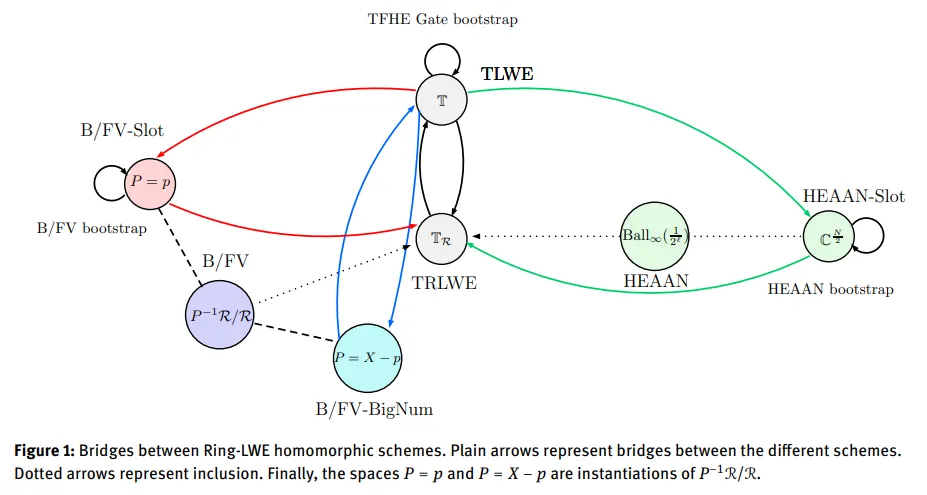
2021 PEGASUS
2021年 PEGASUS: Bridging Polynomial and Non-polynomial Evaluations in Homomorphic Encryption
PEGASUS可以在打包的CKKS密码文和FHEW密码文之间有效地来回切换而无需解密,使得可以在CKKS方面有效地评估算术函数,并在FHEW密码文上评估查找表(也就是非多项式函数)。算法将计算复杂性从线性提高到亚线性。此外转换密钥的大小明显更小,从80千兆字节减少到12兆字节。论文最后提出了PEGASUS的广泛基准,包括sigmoid/ReLU/min/max/division,排序和最大集合。
为了进一步证明PEGASUS的能力,作者开发了两个应用程序:
- 第一个是私有决策树评估,其通信成本比以前基于HE的方法小两个数量级
- 第二个是一个安全的K-means聚类,它能够在几分钟内运行在成千上万的加密样本上,比现有的最佳系统要好14-20倍。据作者所知,这是第一项支持在单服务器环境下使用HE进行实用K-means聚类的工作